---

gnn_quadric : Quadric Discriminant Activation Function.
[Atomic Nodes.]

---

Detailed Description

This node type takes the input variables and produces outputs, corresponding to the cross-multiplication of the inputs:

where , .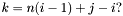

Example:

The resulting terms, combinend with a linear transform, can model quadric decision boundaries (parabola, hyperbola, ellipsoids and spheres), which are richer in structure than classic linear discriminants.

Note:

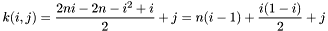
Functions
int	gnn_quadric_f (gnn_node *node, const gsl_vector *x, const gsl_vector *w, gsl_vector *y)
	Computes the output.
int	gnn_quadric_dx (gnn_node *node, const gsl_vector *x, const gsl_vector *w, const gsl_vector *dy, gsl_vector *dx)
	Computes .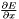
gnn_node *	gnn_quadric_new (int input_size)
	Creates a Quadric Discriminant Transfer function node.

---

Function Documentation

int gnn_quadric_dx (  gnn_node *    node, const gsl_vector *    x, const gsl_vector *    w, const gsl_vector *    dy, gsl_vector *    dx )  [static]

This functions computes the gradient of the Quadric Discriminant activation function, given dy ( ). The function is, Parameters: node  A pointer to a gnn_quadric node. x  The input vector . w  The current parameter vector . dy  The error-backpropagation vector dx  An output vector where the result should be stored. Returns: 0 if suceeded. Definition at line 146 of file gnn_quadric.c.

int gnn_quadric_f (  gnn_node *    node, const gsl_vector *    x, const gsl_vector *    w, gsl_vector *    y )  [static]

This functions evaluates the Quadric Discriminant Transfer function. Parameters: node  A pointer to a gnn_quadric node. x  The input vector . w  The current parameter vector . y  An output vector where the result should be stored. Returns: 0 if succeeded. Definition at line 92 of file gnn_quadric.c.

gnn_node* gnn_quadric_new (  int    input_size )

This function creates a node of the gnn_quadric type. This node produces the second-order terms of its inputs. For a complete review, see gnn_quadric : Quadric Discriminant Activation Function.. Parameters: input_size  The input size . Returns: A pointer to a new gnn_quadric node. Definition at line 208 of file gnn_quadric.c.

---