---

gnn_gcomm : Generalized Committee Convergence Node.
[Atomic Nodes.]

---

Detailed Description

This node type implements the function given by:

where and 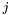are uniquely combined in order to run over all input indexes , and the coefficients are:

Note that this assures that

In other words, this function slices the input vector 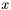into several subvectors of size and performs a weighted sum of them.

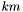If the input vector's size isn't a multiple of the output vector's size, that is, if can't be written as , then the last vector slice will consider only the remaining terms, e.g. if 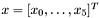and 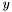is of size then

Schematically, this idea can be depicted as

The function's gradients are:

and for the :

and

where .

Typedefs
typedef _gnn_gcomm	gnn_gcomm
	The structure for a gnn_gcomm : Generalized Committee Convergence Node. node.
Functions
int	gnn_gcomm_f (gnn_node *node, const gsl_vector *x, const gsl_vector *w, gsl_vector *y)
	Computes the output.
int	gnn_gcomm_dx (gnn_node *node, const gsl_vector *x, const gsl_vector *w, const gsl_vector *dy, gsl_vector *dx)
	Computes .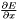
int	gnn_gcomm_dw (gnn_node *node, const gsl_vector *x, const gsl_vector *w, const gsl_vector *dy, gsl_vector *dw)
	Computes .
void	gnn_gcomm_destroy (gnn_node *node)
	Computes the output.
gnn_node *	gnn_gcomm_new (size_t input_size, size_t output_size)
	Creates an generalized committee node.

---

Typedef Documentation

typedef struct _gnn_gcomm gnn_gcomm

This datatype holds the information for a gnn_gcomm : Generalized Committee Convergence Node. node. Basically, it extends the gnn_node with special pointers to get fast accesses to the needed vector slices. Definition at line 48 of file gnn_gcomm.h.

---

Function Documentation

void gnn_gcomm_destroy (  gnn_node *    node )  [static]

Parameters: node  A pointer to the gnn_gcomm : Generalized Committee Convergence Node. node. Definition at line 280 of file gnn_gcomm.c.

int gnn_gcomm_dw (  gnn_node *    node, const gsl_vector *    x, const gsl_vector *    w, const gsl_vector *    dy, gsl_vector *    dw )  [static]

Parameters: node  A pointer to the gnn_gcomm : Generalized Committee Convergence Node. node. x  The input vector . w  The parameter vector . dy  The vector . dx  The output buffer vector . Returns: Returns 0 on success. Definition at line 209 of file gnn_gcomm.c.

int gnn_gcomm_dx (  gnn_node *    node, const gsl_vector *    x, const gsl_vector *    w, const gsl_vector *    dy, gsl_vector *    dx )  [static]

Parameters: node  A pointer to the gnn_gcomm : Generalized Committee Convergence Node. node. x  The input vector . w  The parameter vector . dy  The vector . dx  The output buffer vector . Returns: Returns 0 on success. Definition at line 168 of file gnn_gcomm.c.

int gnn_gcomm_f (  gnn_node *    node, const gsl_vector *    x, const gsl_vector *    w, gsl_vector *    y )  [static]

Parameters: node  A pointer to the gnn_gcomm : Generalized Committee Convergence Node. node. x  The input vector . w  The parameter vector . y  The output buffer vector . Returns: Returns 0 on success. Definition at line 122 of file gnn_gcomm.c.

gnn_node* gnn_gcomm_new (  size_t    input_size, size_t    output_size )

This function creates a node of the gnn_gcomm : Generalized Committee Convergence Node. type. The coefficients are all initialized at the same value. This is equivalent to set the all to . Parameters: input_size  The input size . output_size  The output size . Returns: A pointer to a new gnn_gcomm : Generalized Committee Convergence Node. node. Definition at line 315 of file gnn_gcomm.c.

---