---

gnn_cross_entropy : Cross-Entropy Error Criterion.
[gnn_criterion : Basic Criterion Function.]

---

Detailed Description

This datatype implements the Cross-Entropy criterion, given by

As it can be easily seen, the cross entropy cost function depends on the relative error (instead of the absolute error like in MSE), thus giving to small and large errors te same weight.

The cross entropy criterion fits well in classification problems, where the output encodes the class using binary values; that is, where and for all if the input 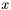corresponds to the -th class.

Defines
#define	GNN_CROSS_ENTROPY_EPS   0.0001
	Minimum value to be evaluated in a logarithm.
Functions
double	gnn_cross_entropy_e (gnn_criterion *crit, const gsl_vector *y, const gsl_vector *t)
	The evaluation function.
int	gnn_cross_entropy_dy (gnn_criterion *crit, const gsl_vector *y, const gsl_vector *t, gsl_vector *dy)
	The gradient evaluation function.
gnn_criterion *	gnn_cross_entropy_new (size_t size)
	Creates a new gnn_cross_entropy criterion.

---

Define Documentation

#define GNN_CROSS_ENTROPY_EPS   0.0001

The evaluation of the cross entropy criterion has some tricky parts. Whenever the natural logarithm of a very small quantity is to be taken, then this value sets the limit. Definition at line 48 of file gnn_cross_entropy.h.

---

Function Documentation

int gnn_cross_entropy_dy (  gnn_criterion *    crit, const gsl_vector *    y, const gsl_vector *    t, gsl_vector *    dy )

This function implements the gnn_cross_entropy criterion's gradient evaluation function given by Parameters: crit  A pointer to a gnn_cross_entropy criterion. y  A pointer to an estimation vector . t  A pointer to the desired target vector . dy  A pointer to a buffer vector where the result should be placed. Returns: Returns 0 if succeeded. Definition at line 145 of file gnn_cross_entropy.c.

double gnn_cross_entropy_e (  gnn_criterion *    crit, const gsl_vector *    y, const gsl_vector *    t )

This function corresponds to the evaluation of the cross entropy criterion. Parameters: crit  A pointer to a gnn_cross_entropy criterion. y  A pointer to an estimation vector . t  A pointer to the desired target vector . Returns: A real number corresponding to the value of the criterion. Definition at line 89 of file gnn_cross_entropy.c.

gnn_criterion* gnn_cross_entropy_new (  size_t    size )

This function creates a new gnn_cross_entropy criterion of the given size. Parameters: size  The size of the estimation and the target vector and . Returns: Returns a pointer to a new gnn_cross_entropy or NULL if failed. Definition at line 204 of file gnn_cross_entropy.c.

---