libgnn Quickstart Guide

The following is a simple guide for libgnn beginners. It should introduce you to libgnn basics.

libgnn is a very low-level C library for GRM's, but it's very versatile.

Main Concepts

In libgnn, there are four different kind of objects you need to know about:

The idea here is quite simple. First, you should build a GRM. The GRM can be trained, which consists in adjusting its internal parameters, in order to aproximate the function represented by the input-output pairs given in the training set. The criterion measures the performance, and can be something like mean-square-error or cross-entropy, per example. The trainer then uses a gradient based algorithm to adjust the GRM's parameters.

Installation

First, obtain and install the Gnu Scientific Library. As far as I know, it now runs on all known platforms. So should libgnn too ;-). Please note that GSL needs a BLAS lib, it can be the one contained with the GSL distro, or another one like atlas.

At the time, the way to go is to compile libgnn at the command line executing make. You shouldn't experience any problem. If something goes wrong, edit the Makefile. The only things you should modify are the LIBS and/or the INCS variables.

If the compilation went fine, then you should have obtained a libgnn.a file as a result. Copy it into your compiler's lib directory.

Then, copy the header files contained in the include directory into your compiler's include directory. Voilą! (Not very pretty right now, but it works!)

A simple program.

Let's build a simple neural net. Download the test file. The test file contains a simple command-line program skeleton. You have to fill out three functions which describe the GRM, the criterion and the trainer. Once done and compiled, you'll be able to execute the programm like this:

    % mynet train paramFile.txt inputFile.txt targetFile.txt 1000

which trains a GRM using the inputs in inputFile.txt and associated targets in targetFile.txt during 1000 epochs (iterations), and saves the resulting parameters in paramFile.

You can then resume the training executing the program with the same parameters. The program first checks if paramFile.txt exists, and if yes, it loads the parameters from the file and then it starts the training procedure.

If you're done with the training, then you can use the program to evaluate the result of given inputs:

    % mynet eval paramFile.txt inputs.txt outputs.txt

This loads the parameters from paramFile.txt, loads the inputs stored in inputs.txt, computes the outputs, and saves them into outputs.txt.

Thus, the test file is quite handy if you need to implement a GRM in few minutes. Of course, you could code a more sophisticated framework. If you do so, please let me know ;-)

Lets look at the test file:

/* Include Files */

#include <stdio.h>
#include <stdlib.h>
#include <strings.h>

#include <libgnn.h>

...some other things here...


/* Implementation. */

gnn_node*
libgnn_build_machine ()
{
   /* return a gnn_node here */
}

gnn_criterion*
libgnn_build_criterion ()
{
    /* return a gnn_criterion here */
}

gnn_trainer*
libgnn_build_trainer (gnn_node *machine,
                      gnn_criterion *crit, gnn_dataset *trainset)
{
    /* return a gnn_trainer here */
}

int
libgnn_trainloop (gnn_trainer *trainer, size_t maxEpochs)
{
    double error;
    size_t epoch;
    
    gnn_trainer_reset (trainer);
    epoch = gnn_trainer_get_epoch (trainer);
    
    for (; epoch <= maxEpochs; epoch = gnn_trainer_get_epoch (trainer))
    {
        gnn_trainer_train (trainer);
        error = gnn_trainer_get_epoch_cost (trainer);
        printf ("Epoch: %3d - Error : %10.6f \r", epoch, error);
    }
    printf ("\n");
    
    return 0;
}

...

There are 3 empty functions here: libgnn_build_machine, libgnn_build_criterion and libgnn_build_trainer. Let's fill them out.

Breiman Training Set

The downloaded file contains a training set: The Breiman Base. Right now, it doesn't matter what it is, but you should know that the training set is a quite complex one (waveforms), and it contains 40 input variables and 3 outputs. From the input features, the first twenty actually contain valid data, while the last twenty ones are only noise. The input set is contained in breiman_inputs.txt:

-0.087148  0.008913 -0.026853  0.198227  0.188818  0.100683 ... 
 0.013232  0.001576 -0.022927  0.009549  0.022941  0.039676 ...
-0.038554 -0.067923 -0.049237 -0.071115 -0.080561 -0.038602 ...
-0.025637  0.064785  0.075002 -0.020713  0.051575  0.007053 ...
 0.040446 -0.011434 -0.003054  0.065561  0.110038  0.324551 ...
   ...       ...       ...       ...       ...       ...

Each input has a corresponding class label. There are three possible classes. The class labels (contained in breiman_targets.txt) are coded as follows:

1.000000 0.000000 0.000000 
0.000000 1.000000 0.000000 
0.000000 0.000000 1.000000 
1.000000 0.000000 0.000000 
  ...      ...      ...

...that is, the components are zero, except at the i-th position, meaning that the sample corresponds to the i-th class. So, the targets are vectors of size 3. We will use this training set during this guide.

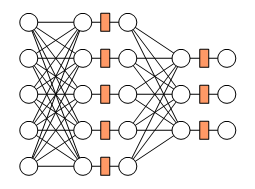
Let's build a Gradient Retropropagation Machine!

Ok. Now you should build your first GRM. The Breiman Base needs a GRM with 40 inputs and 3 outputs. We could use a 2-layer feedforward perceptron like the following one, but having 40 inputs:

The light red boxes represent sigmoidal activation functions. It's easy to see that this neural net can be decomposed into 4 modules:

Lets say that we want to have 20 hidden units. This is coded as:

    /* Declare pointers to the 4 modules. */
    gnn_node *w1;
    gnn_node *w2;
    gnn_node *s1;
    gnn_node *s2;
    
    /* Now create them. */

    /* Create a weight layer with 40 inputs and 20 outputs. */
    w1 = gnn_weight_new (40, 20);
    gnn_weight_init (w1);

    /* Now a logistic sigmoid activation layer,
       which should have 20 inputs and 20 outputs. */
    s1 = gnn_logistic_standard_new (20);

    /* Create the second weight layer which
       takes 20 inputs and produces 3 outputs. */
    w2 = gnn_weight_new (20, 3);
    gnn_weight_init (w2);

    /* Finally, another logistic sigmoid
       layer with 3 inputs and outputs. */
    s2 = gnn_logistic_standard_new (3);

Please note that all nodes, although they represent different kind of functions, they're all gnn_nodes.

Now, these 4 layers should be connected to form the neural net. This is done by creating a new gnn_node:

    gnn_node *neuralNet;

    neuralNet = gnn_serial_new (4, w1, s1, w2, s2);

That's all! gnn_serial is a special kind of gnn_node, called constructor nodes.

Now, put all the above code into the libgnn_build_machine function (I've added some error-checking code):

gnn_node*
libgnn_build_machine ()
{
    gnn_node *w1;
    gnn_node *w2;
    gnn_node *s1;
    gnn_node *s2;
    gnn_node *neuralNet;
    
    w1 = gnn_weight_new (40, 20);
    s1 = gnn_logistic_standard_new (20);
    w2 = gnn_weight_new (20, 3);
    s2 = gnn_logistic_standard_new (3);
    if (w1 == NULL || w2 == NULL || s1 == NULL || s2 == NULL)
    {
        fprintf (stderr, "Couldn't build one or more components "
                         "of the neural net.\n");
        return NULL;
    }
    
    gnn_weight_init (w1);
    gnn_weight_init (w2);
    
    neuralNet = gnn_serial_new (4, w1, s1, w2, s2);
    if (nn == NULL)
    {
        fprintf (stderr, "Couldn't build neural net.\n");
        return NULL;
    }
    
    return neuralNet;
}

We have now completed the first function. We need to fill out the other ones.

Criterions

We need to specify now a criterion to evaluate the permormance of the neural net built in the previous section. You can choose one of libgnn's built-in criterions, like mean-square-error or cross-entropy:

    gnn_criterion *criterion;
    
    /* If you want a mse criterion: */
    criterion = gnn_mse_new (3);

    /* If you want to use cross-entropy: */
    criterion = gnn_cross_entropy_new (3);

When building a criterion, you should specify the size of the machine's outputs. In the previous case, we have seen that the outputs are of size 3, that is, an output vector of three components.

Put now the corresponding code into the libgnn_build_criterion function:

gnn_criterion*
libgnn_build_criterion ()
{
    return gnn_cross_entropy_new (3);
}

Building the trainer

As in the previous case, there are many different types of trainers in libgnn. Just choose one and put its building code into the libgnn_build_trainer function:

gnn_trainer*
libgnn_build_trainer (gnn_node *machine,
                      gnn_criterion *crit, gnn_dataset *trainset)
{
    return gnn_conjugate_gradient_new (machine, crit, trainset);
}

In this case, we've built a trainer that uses the Conjugate Gradients algorithm to adjust the machine's parameters. But there are many others, like Gradient Descent, Gradient Descent with Momentum, BFGS, RProp, etc.

Compile it.

Save the code as myexample.c. Now, compile it:

    % gcc myexample.c -lgnn -lgsl -lgslcblas -lm -o myexample

If your system is apropiately configurated, then it should work. If not, then it may be necessary to include some additional flags, like:

    % gcc myexample.c -I<path-to-libgnn-headers> -I<path-to-gsl-headers> -lgnn -lgsl -lgslcblas -lm -o myexample

Test it.

Since you've used the simple program skeleton, you can execute it like this:

    % myexample train paramFile.txt breiman_inputs.txt breiman_targets.txt

© 2004 Pedro Ortega C.